空飛ぶロボットのつくりかた

ロボットをつくるために必要な技術をまとめます。ロボットの未来についても考えたりします。

機械学習のお勉強(多層パーセプトロン)

Machine Learning Python

人口知能で人の仕事は奪われるの？

f:id:robonchu:20171209080830p:plain

My answer is ... the end of this blog ↓

教科書

GitHub - scikit-learn/scikit-learn: scikit-learn: machine learning in Python

単層ニューラルネットワーク(ADALINE)の復習

f:id:robonchu:20171209080857p:plain

  • 重みの更新式
    • w := w + \nabla w , \nabla w = - \eta \nabla J(w)
  • コスト関数(誤差平方和)J(w)
    • J(w) = \frac{1}{2} \Sigma_{i} (y^{(i)} - a^{(i)} )^{2}
    • \frac{\partial J(w)}{\partial w_{j}} = - \Sigma_{i} (y^{(i)} - a^{(i)} ) x_{j}^{(i)}　
    • \phi(z) = z = a　← ADLINEの場合こうなる
    • y : クラスラベル、　a : activation,ニューロンの活性(線形関数)、　\phi : 活性化関数　
    • z = \Sigma_{j} w_{j} x_{j} = \bf {w^{T} x}　、
  • クラスラベルの予測
    • \hat{y} = \begin{cases} 1 \ \ (z >= 0) \\ -1 \ \ (otherwise) \end{cases}

多層パーセプトロン(Multi-Layer Perceptron )のアーキテクチャ

f:id:robonchu:20171209085301p:plain

上図のように隠れ層がひとつ以上あるネットワークは「ディープ」人口ニューラルネットワークと呼ばれる。

隠れ層の数を増やすとどうなるの？

隠れ層を増やすと表現力は増すが、学習計算の過程で勾配消失問題等も発生する。 如何に表現力を増しつつ、学習過程で誤差情報を伝播させていくかが重要。

f:id:robonchu:20171209091009p:plain

参考：Mind で Neural Network (準備編2) 順伝播・逆伝播 図解 - Qiita

MLPの学習のプロセス

  1. 入力層を出発として訓練データのパターンを順伝播し、出力生成。

  2. 出力を使ってコスト関数を用いて、誤差を計算。この誤差の最小化が目的。

  3. 誤差を逆伝播し、ネットワークの各重みに関する偏導関数を求め、モデルの更新

予測時はこの重みを用いて順伝播で出力を生成する。

つまり、学習の目的は最適関数を最小化するようなネットワークの重み(パラメータ)を計算すること。

順伝播によるニューラルネットワークの活性化

z^{(2)}_{1} = a^{(1)}_{0} w^{(1)}_{1,0} + a^{(1)}_{1} w^{(1)}_{1,1} + ・・・ + a^{(1)}_{m} w^{(1)}_{1,m}

a^{(2)}_{1} = \phi {(z^{(2)}_{1} )}

ここでのポイントは学習のために、活性化関数 \phi (・)が微分可能でなければならない

複雑な問題を解く際は、非線形の活性化関数であるシグモイド関数等が使われる。

\phi(z) = \frac{1}{1+e^{-z}}

f:id:robonchu:20171209093822p:plain

これを微分すると

\phi ' = (1 - \phi) \phi

ととても綺麗な形になるよ。

参考：　シグモイド関数を微分する - のんびりしているエンジニアの日記

他にどんな活性化関数があるの？

f:id:robonchu:20171209094222p:plain

このRelu関数がよく使わている。　But ... 2017/10~にswishと呼ばれる新たな活性化関数が発表され、効果がよさ気↓

f:id:robonchu:20171209094401p:plain

式は \phi(z) = x ・ \sigma(x) と簡単。微分も簡単。

MLPを使って手書き文字を分類してみる

mnistのダウンロードとロード

MNIST handwritten digit database, Yann LeCun, Corinna Cortes and Chris Burges

import os
import struct
import numpy as np
import gzip
 
def load_mnist(path, kind='train'):
    """Load MNIST data from `path`"""
    labels_path = os.path.join(path, 
                               '%s-labels-idx1-ubyte.gz' % kind)
    images_path = os.path.join(path, 
                               '%s-images-idx3-ubyte.gz' % kind)
        
    with gzip.open(labels_path, 'rb') as lbpath:
        lbpath.read(8)
        buffer = lbpath.read()
        labels = np.frombuffer(buffer, dtype=np.uint8)

    with gzip.open(images_path, 'rb') as imgpath:
        imgpath.read(16)
        buffer = imgpath.read()
        images = np.frombuffer(buffer, 
                               dtype=np.uint8).reshape(
            len(labels), 784).astype(np.float64)
 
    return images, labels

X_train, y_train = load_mnist('mnist/', kind='train')
print('Rows: %d, columns: %d' % (X_train.shape[0], X_train.shape[1]))

X_test, y_test = load_mnist('mnist/', kind='t10k')
print('Rows: %d, columns: %d' % (X_test.shape[0], X_test.shape[1]))

表示結果

Rows: 60000, columns: 784
Rows: 10000, columns: 784

クラスラベルが0~9の画像を表示

import matplotlib.pyplot as plt

fig, ax = plt.subplots(nrows=2, ncols=5, sharex=True, sharey=True,)
ax = ax.flatten()
for i in range(10):
    img = X_train[y_train == i][0].reshape(28, 28)
    ax[i].imshow(img, cmap='Greys', interpolation='nearest')

ax[0].set_xticks([])
ax[0].set_yticks([])
plt.tight_layout()
# plt.savefig('./figures/mnist_all.png', dpi=300)
plt.show()

f:id:robonchu:20171209102025p:plain

クラスラベルは7の画像を表示

fig, ax = plt.subplots(nrows=5, ncols=5, sharex=True, sharey=True,)
ax = ax.flatten()
for i in range(25):
    img = X_train[y_train == 7][i].reshape(28, 28)
    ax[i].imshow(img, cmap='Greys', interpolation='nearest')

ax[0].set_xticks([])
ax[0].set_yticks([])
plt.tight_layout()
# plt.savefig('./figures/mnist_7.png', dpi=300)
plt.show()

f:id:robonchu:20171216100923p:plain

前処理、モデル構築を行う上で、ここのデータの特性をしることがとても重要！！！

多層パーセプトロンの実装

import numpy as np
from scipy.special import expit
import sys


class NeuralNetMLP(object):
    """ Feedforward neural network / Multi-layer perceptron classifier.

    Parameters
    ------------
    n_output : int
        Number of output units, should be equal to the
        number of unique class labels.
    n_features : int
        Number of features (dimensions) in the target dataset.
        Should be equal to the number of columns in the X array.
    n_hidden : int (default: 30)
        Number of hidden units.
    l1 : float (default: 0.0)
        Lambda value for L1-regularization.
        No regularization if l1=0.0 (default)
    l2 : float (default: 0.0)
        Lambda value for L2-regularization.
        No regularization if l2=0.0 (default)
    epochs : int (default: 500)
        Number of passes over the training set.
    eta : float (default: 0.001)
        Learning rate.
    alpha : float (default: 0.0)
        Momentum constant. Factor multiplied with the
        gradient of the previous epoch t-1 to improve
        learning speed
        w(t) := w(t) - (grad(t) + alpha*grad(t-1))
    decrease_const : float (default: 0.0)
        Decrease constant. Shrinks the learning rate
        after each epoch via eta / (1 + epoch*decrease_const)
    shuffle : bool (default: True)
        Shuffles training data every epoch if True to prevent circles.
    minibatches : int (default: 1)
        Divides training data into k minibatches for efficiency.
        Normal gradient descent learning if k=1 (default).
    random_state : int (default: None)
        Set random state for shuffling and initializing the weights.

    Attributes
    -----------
    cost_ : list
      Sum of squared errors after each epoch.

    """
    def __init__(self, n_output, n_features, n_hidden=30,
                 l1=0.0, l2=0.0, epochs=500, eta=0.001,
                 alpha=0.0, decrease_const=0.0, shuffle=True,
                 minibatches=1, random_state=None):

        np.random.seed(random_state)
        self.n_output = n_output
        self.n_features = n_features
        self.n_hidden = n_hidden
        self.w1, self.w2 = self._initialize_weights()
        self.l1 = l1
        self.l2 = l2
        self.epochs = epochs
        self.eta = eta
        self.alpha = alpha
        self.decrease_const = decrease_const
        self.shuffle = shuffle
        self.minibatches = minibatches

    def _encode_labels(self, y, k):
        """Encode labels into one-hot representation

        Parameters
        ------------
        y : array, shape = [n_samples]
            Target values.

        Returns
        -----------
        onehot : array, shape = (n_labels, n_samples)

        """
        onehot = np.zeros((k, y.shape[0]))
        for idx, val in enumerate(y):
            onehot[val, idx] = 1.0
        return onehot

    def _initialize_weights(self):
        """Initialize weights with small random numbers."""
        w1 = np.random.uniform(-1.0, 1.0,
                               size=self.n_hidden*(self.n_features + 1))
        w1 = w1.reshape(self.n_hidden, self.n_features + 1)
        w2 = np.random.uniform(-1.0, 1.0,
                               size=self.n_output*(self.n_hidden + 1))
        w2 = w2.reshape(self.n_output, self.n_hidden + 1)
        return w1, w2

    def _sigmoid(self, z):
        """Compute logistic function (sigmoid)

        Uses scipy.special.expit to avoid overflow
        error for very small input values z.

        """
        # return 1.0 / (1.0 + np.exp(-z))
        return expit(z)

    def _sigmoid_gradient(self, z):
        """Compute gradient of the logistic function"""
        sg = self._sigmoid(z)
        return sg * (1.0 - sg)

    def _add_bias_unit(self, X, how='column'):
        """Add bias unit (column or row of 1s) to array at index 0"""
        if how == 'column':
            X_new = np.ones((X.shape[0], X.shape[1] + 1))
            X_new[:, 1:] = X
        elif how == 'row':
            X_new = np.ones((X.shape[0] + 1, X.shape[1]))
            X_new[1:, :] = X
        else:
            raise AttributeError('`how` must be `column` or `row`')
        return X_new

    def _feedforward(self, X, w1, w2):
        """Compute feedforward step

        Parameters
        -----------
        X : array, shape = [n_samples, n_features]
            Input layer with original features.
        w1 : array, shape = [n_hidden_units, n_features]
            Weight matrix for input layer -> hidden layer.
        w2 : array, shape = [n_output_units, n_hidden_units]
            Weight matrix for hidden layer -> output layer.

        Returns
        ----------
        a1 : array, shape = [n_samples, n_features+1]
            Input values with bias unit.
        z2 : array, shape = [n_hidden, n_samples]
            Net input of hidden layer.
        a2 : array, shape = [n_hidden+1, n_samples]
            Activation of hidden layer.
        z3 : array, shape = [n_output_units, n_samples]
            Net input of output layer.
        a3 : array, shape = [n_output_units, n_samples]
            Activation of output layer.

        """
        a1 = self._add_bias_unit(X, how='column')
        z2 = w1.dot(a1.T)
        a2 = self._sigmoid(z2)
        a2 = self._add_bias_unit(a2, how='row')
        z3 = w2.dot(a2)
        a3 = self._sigmoid(z3)
        return a1, z2, a2, z3, a3

    def _L2_reg(self, lambda_, w1, w2):
        """Compute L2-regularization cost"""
        return (lambda_/2.0) * (np.sum(w1[:, 1:] ** 2) +
                                np.sum(w2[:, 1:] ** 2))

    def _L1_reg(self, lambda_, w1, w2):
        """Compute L1-regularization cost"""
        return (lambda_/2.0) * (np.abs(w1[:, 1:]).sum() +
                                np.abs(w2[:, 1:]).sum())

    def _get_cost(self, y_enc, output, w1, w2):
        """Compute cost function.

        Parameters
        ----------
        y_enc : array, shape = (n_labels, n_samples)
            one-hot encoded class labels.
        output : array, shape = [n_output_units, n_samples]
            Activation of the output layer (feedforward)
        w1 : array, shape = [n_hidden_units, n_features]
            Weight matrix for input layer -> hidden layer.
        w2 : array, shape = [n_output_units, n_hidden_units]
            Weight matrix for hidden layer -> output layer.

        Returns
        ---------
        cost : float
            Regularized cost.

        """
        term1 = -y_enc * (np.log(output))
        term2 = (1.0 - y_enc) * np.log(1.0 - output)
        cost = np.sum(term1 - term2)
        L1_term = self._L1_reg(self.l1, w1, w2)
        L2_term = self._L2_reg(self.l2, w1, w2)
        cost = cost + L1_term + L2_term
        return cost

    def _get_gradient(self, a1, a2, a3, z2, y_enc, w1, w2):
        """ Compute gradient step using backpropagation.

        Parameters
        ------------
        a1 : array, shape = [n_samples, n_features+1]
            Input values with bias unit.
        a2 : array, shape = [n_hidden+1, n_samples]
            Activation of hidden layer.
        a3 : array, shape = [n_output_units, n_samples]
            Activation of output layer.
        z2 : array, shape = [n_hidden, n_samples]
            Net input of hidden layer.
        y_enc : array, shape = (n_labels, n_samples)
            one-hot encoded class labels.
        w1 : array, shape = [n_hidden_units, n_features]
            Weight matrix for input layer -> hidden layer.
        w2 : array, shape = [n_output_units, n_hidden_units]
            Weight matrix for hidden layer -> output layer.

        Returns
        ---------
        grad1 : array, shape = [n_hidden_units, n_features]
            Gradient of the weight matrix w1.
        grad2 : array, shape = [n_output_units, n_hidden_units]
            Gradient of the weight matrix w2.

        """
        # backpropagation
        sigma3 = a3 - y_enc
        z2 = self._add_bias_unit(z2, how='row')
        sigma2 = w2.T.dot(sigma3) * self._sigmoid_gradient(z2)
        sigma2 = sigma2[1:, :]
        grad1 = sigma2.dot(a1)
        grad2 = sigma3.dot(a2.T)

        # regularize
        grad1[:, 1:] += self.l2 * w1[:, 1:]
        grad1[:, 1:] += self.l1 * np.sign(w1[:, 1:])
        grad2[:, 1:] += self.l2 * w2[:, 1:]
        grad2[:, 1:] += self.l1 * np.sign(w2[:, 1:])

        return grad1, grad2

    def predict(self, X):
        """Predict class labels

        Parameters
        -----------
        X : array, shape = [n_samples, n_features]
            Input layer with original features.

        Returns:
        ----------
        y_pred : array, shape = [n_samples]
            Predicted class labels.

        """
        if len(X.shape) != 2:
            raise AttributeError('X must be a [n_samples, n_features] array.\n'
                                 'Use X[:,None] for 1-feature classification,'
                                 '\nor X[[i]] for 1-sample classification')

        a1, z2, a2, z3, a3 = self._feedforward(X, self.w1, self.w2)
        y_pred = np.argmax(z3, axis=0)
        return y_pred

    def fit(self, X, y, print_progress=False):
        """ Learn weights from training data.

        Parameters
        -----------
        X : array, shape = [n_samples, n_features]
            Input layer with original features.
        y : array, shape = [n_samples]
            Target class labels.
        print_progress : bool (default: False)
            Prints progress as the number of epochs
            to stderr.

        Returns:
        ----------
        self

        """
        self.cost_ = []
        X_data, y_data = X.copy(), y.copy()
        y_enc = self._encode_labels(y, self.n_output)

        delta_w1_prev = np.zeros(self.w1.shape)
        delta_w2_prev = np.zeros(self.w2.shape)

        for i in range(self.epochs):

            # adaptive learning rate
            self.eta /= (1 + self.decrease_const*i)

            if print_progress:
                sys.stderr.write('\rEpoch: %d/%d' % (i+1, self.epochs))
                sys.stderr.flush()

            if self.shuffle:
                idx = np.random.permutation(y_data.shape[0])
                X_data, y_enc = X_data[idx], y_enc[:, idx]

            mini = np.array_split(range(y_data.shape[0]), self.minibatches)
            for idx in mini:

                # feedforward
                a1, z2, a2, z3, a3 = self._feedforward(X_data[idx],
                                                       self.w1,
                                                       self.w2)
                cost = self._get_cost(y_enc=y_enc[:, idx],
                                      output=a3,
                                      w1=self.w1,
                                      w2=self.w2)
                self.cost_.append(cost)

                # compute gradient via backpropagation
                grad1, grad2 = self._get_gradient(a1=a1, a2=a2,
                                                  a3=a3, z2=z2,
                                                  y_enc=y_enc[:, idx],
                                                  w1=self.w1,
                                                  w2=self.w2)

                delta_w1, delta_w2 = self.eta * grad1, self.eta * grad2
                self.w1 -= (delta_w1 + (self.alpha * delta_w1_prev))
                self.w2 -= (delta_w2 + (self.alpha * delta_w2_prev))
                delta_w1_prev, delta_w2_prev = delta_w1, delta_w2

        return self

one-hot 表現

    def _encode_labels(self, y, k):
        """Encode labels into one-hot representation

        Parameters
        ------------
        y : array, shape = [n_samples]
            Target values.

        Returns
        -----------
        onehot : array, shape = (n_labels, n_samples)

        """
        onehot = np.zeros((k, y.shape[0]))
        for idx, val in enumerate(y):
            onehot[val, idx] = 1.0
        return onehot

参考： One hot表現を実装してみた - Qiita

重みの初期化

    def _initialize_weights(self):
        """Initialize weights with small random numbers."""
        w1 = np.random.uniform(-1.0, 1.0,
                               size=self.n_hidden*(self.n_features + 1))
        w1 = w1.reshape(self.n_hidden, self.n_features + 1)
        w2 = np.random.uniform(-1.0, 1.0,
                               size=self.n_output*(self.n_hidden + 1))
        w2 = w2.reshape(self.n_output, self.n_hidden + 1)
        return w1, w2

ランダムに重みを初期化。

NumPyの使い方（１２） 乱数、random - Remrinのpython攻略日記

ここが重要だったりする。非線形性が強く、局所解がたくさんあるため。

少ない画像から画像分類を学習させる方法（kerasで転移学習：fine tuning）

シグモイド関数とその微分

    def _sigmoid(self, z):
        """Compute logistic function (sigmoid)

        Uses scipy.special.expit to avoid overflow
        error for very small input values z.

        """
        # return 1.0 / (1.0 + np.exp(-z))
        return expit(z)

    def _sigmoid_gradient(self, z):
        """Compute gradient of the logistic function"""
        sg = self._sigmoid(z)
        return sg * (1.0 - sg)

他にもたくさんの活性化関数があるよ

最新の性能の良い、活性化関数はswish。

参考：

活性化関数ReLUについてとReLU一族【追記あり】 - Qiita ← Good!!!

活性化関数のまとめ（ステップ、シグモイド、ReLU、ソフトマックス、恒等関数） - Qiita

活性化関数 Swish - Qiita

順伝播

    def _feedforward(self, X, w1, w2):
        """Compute feedforward step

        Parameters
        -----------
        X : array, shape = [n_samples, n_features]
            Input layer with original features.
        w1 : array, shape = [n_hidden_units, n_features]
            Weight matrix for input layer -> hidden layer.
        w2 : array, shape = [n_output_units, n_hidden_units]
            Weight matrix for hidden layer -> output layer.

        Returns
        ----------
        a1 : array, shape = [n_samples, n_features+1]
            Input values with bias unit.
        z2 : array, shape = [n_hidden, n_samples]
            Net input of hidden layer.
        a2 : array, shape = [n_hidden+1, n_samples]
            Activation of hidden layer.
        z3 : array, shape = [n_output_units, n_samples]
            Net input of output layer.
        a3 : array, shape = [n_output_units, n_samples]
            Activation of output layer.

        """
        a1 = self._add_bias_unit(X, how='column')
        z2 = w1.dot(a1.T)
        a2 = self._sigmoid(z2)
        a2 = self._add_bias_unit(a2, how='row')
        z3 = w2.dot(a2)
        a3 = self._sigmoid(z3)
        return a1, z2, a2, z3, a3

L1正規化、L2正規化

    def _L2_reg(self, lambda_, w1, w2):
        """Compute L2-regularization cost"""
        return (lambda_/2.0) * (np.sum(w1[:, 1:] ** 2) +
                                np.sum(w2[:, 1:] ** 2))

    def _L1_reg(self, lambda_, w1, w2):
        """Compute L1-regularization cost"""
        return (lambda_/2.0) * (np.abs(w1[:, 1:]).sum() +
                                np.abs(w2[:, 1:]).sum())

参考：

RでL1 / L2正則化を実践する - 六本木で働くデータサイエンティストのブログ

コスト関数

ロジスティック関数

  • J(w) = - [ \Sigma_{i=1}^{n} y^{(i)} log (a^{(i)}) + (1 - y^{(i)}) log (1- a^{(i)}) ] + \lambda \Sigma_{j=1}^{m} w_{j}^{2} + \lambda \Sigma_{j=1}^{m} | w_{j} |

  • a^{(i)} = \phi (z^{(i)})

参考： ロジスティック回帰のコスト関数を眺める - y_uti のブログ

    def _get_cost(self, y_enc, output, w1, w2):
        """Compute cost function.

        Parameters
        ----------
        y_enc : array, shape = (n_labels, n_samples)
            one-hot encoded class labels.
        output : array, shape = [n_output_units, n_samples]
            Activation of the output layer (feedforward)
        w1 : array, shape = [n_hidden_units, n_features]
            Weight matrix for input layer -> hidden layer.
        w2 : array, shape = [n_output_units, n_hidden_units]
            Weight matrix for hidden layer -> output layer.

        Returns
        ---------
        cost : float
            Regularized cost.

        """
        term1 = -y_enc * (np.log(output))
        term2 = (1.0 - y_enc) * np.log(1.0 - output)
        cost = np.sum(term1 - term2)
        L1_term = self._L1_reg(self.l1, w1, w2)
        L2_term = self._L2_reg(self.l2, w1, w2)
        cost = cost + L1_term + L2_term
        return cost

誤差逆伝播

上記のコスト関数を最小化することが目的であるので、ネットワークのすべての層の重み事に、行列wの偏微分係数を計算する必要がある。

  • \frac{\partial J(w)}{\partial w_{j,i}^{(l)}}

ここで誤差逆伝播を用いると、コスト関数を最小化するための偏微分係数が計算できる。

w は複数の行列で構成されている　↓

f:id:robonchu:20171216104025p:plain

誤差逆伝播の計算方法

  1. フォワードプロパゲーション f:id:robonchu:20171216104521p:plain

  2. フォワードプロパゲーションの出力とラベルにより、誤差ベクトルを計算（証明は省略）

    • \sigma^{(3)} = a^{(3)} - y
    • \sigma^{(2)} = (w^{(2)})^{T} \sigma^{(3)} * \frac{\partial \phi(z^{(2)})}{\partial z^{(2)}} (*は要素ごとの掛け算)
      • \frac{\partial \phi(z^{(2)})}{\partial z^{(2)}} = (a^{(2)} * (1 - a^{(2)}) )

  3. コスト関数の変微分係数を求める（正規化なしバージョン）

    • \frac{\partial J(w)}{\partial w_{j,i}^{(l)}} = a_{j}^{(l)} \sigma_{i}^{(l+1)}

  4. 重みの更新

    • w^{(l)} := w^{(l)} - \eta \frac{\partial J(w)}{\partial w^{(l)}}

f:id:robonchu:20171216111730p:plain

参考： Pythonで 多層パーセプトロン を実装する | ZABURO app

    def _get_gradient(self, a1, a2, a3, z2, y_enc, w1, w2):
        """ Compute gradient step using backpropagation.

        Parameters
        ------------
        a1 : array, shape = [n_samples, n_features+1]
            Input values with bias unit.
        a2 : array, shape = [n_hidden+1, n_samples]
            Activation of hidden layer.
        a3 : array, shape = [n_output_units, n_samples]
            Activation of output layer.
        z2 : array, shape = [n_hidden, n_samples]
            Net input of hidden layer.
        y_enc : array, shape = (n_labels, n_samples)
            one-hot encoded class labels.
        w1 : array, shape = [n_hidden_units, n_features]
            Weight matrix for input layer -> hidden layer.
        w2 : array, shape = [n_output_units, n_hidden_units]
            Weight matrix for hidden layer -> output layer.

        Returns
        ---------
        grad1 : array, shape = [n_hidden_units, n_features]
            Gradient of the weight matrix w1.
        grad2 : array, shape = [n_output_units, n_hidden_units]
            Gradient of the weight matrix w2.

        """
        # backpropagation
        sigma3 = a3 - y_enc
        z2 = self._add_bias_unit(z2, how='row')
        sigma2 = w2.T.dot(sigma3) * self._sigmoid_gradient(z2)
        sigma2 = sigma2[1:, :]
        grad1 = sigma2.dot(a1)
        grad2 = sigma3.dot(a2.T)

        # regularize
        grad1[:, 1:] += self.l2 * w1[:, 1:]
        grad1[:, 1:] += self.l1 * np.sign(w1[:, 1:])
        grad2[:, 1:] += self.l2 * w2[:, 1:]
        grad2[:, 1:] += self.l1 * np.sign(w2[:, 1:])

        return grad1, grad2

誤差逆伝播に対する直感を養う

自動微分（順伝播、逆伝播）の考え方↓　ものすごくわかりやすい！

計算グラフの微積分：バックプロパゲーションを理解する | POSTD

一言で言うと、誤差逆伝播を用いると計算コストが低くなる。

参考： 誤差逆伝播法を計算グラフを使って分かりやすく解説する - DeepAge

予測

    def predict(self, X):
        """Predict class labels

        Parameters
        -----------
        X : array, shape = [n_samples, n_features]
            Input layer with original features.

        Returns:
        ----------
        y_pred : array, shape = [n_samples]
            Predicted class labels.

        """
        if len(X.shape) != 2:
            raise AttributeError('X must be a [n_samples, n_features] array.\n'
                                 'Use X[:,None] for 1-feature classification,'
                                 '\nor X[[i]] for 1-sample classification')

        a1, z2, a2, z3, a3 = self._feedforward(X, self.w1, self.w2)
        y_pred = np.argmax(z3, axis=0)
        return y_pred

最後argmaxで予測ラベルを算出しているが、softmaxを用いるとそれぞれのクラスの確率を出すことも可能。

参考： Softmaxって何をしてるの？ - 画像処理とか機械学習とか

データのシャッフル

            if self.shuffle:
                idx = np.random.permutation(y_data.shape[0])
                X_data, y_enc = X_data[idx], y_enc[:, idx]

トレーニングデータをシャッフルすることでアルゴリズムを循環しないようにする

適応学習率

            # adaptive learning rate
            self.eta /= (1 + self.decrease_const*i)

参考： 勾配降下法の最適化アルゴリズムを概観する | POSTD

重みの更新方法(勾配法)

                delta_w1, delta_w2 = self.eta * grad1, self.eta * grad2
                self.w1 -= (delta_w1 + (self.alpha * delta_w1_prev))
                self.w2 -= (delta_w2 + (self.alpha * delta_w2_prev))
                delta_w1_prev, delta_w2_prev = delta_w1, delta_w2

  1. SGD

    • W = W - \eta \frac{\partial J(W)}{\partial W}

  2. Momentum

    • W = W_{i} + \alpha \Delta W_{i-1} - \eta \frac{\partial J(W_{i})}{\partial W_{i}}

参考：

勾配降下法の最適化アルゴリズムを概観する | POSTD ←Good!!!

AdaGrad, RMSProp, Adam, ND-Adam, AMSGrad - Qiita

最適化手法について—SGDからYellowFinまで— | moskomule log

トレーニング

nn = NeuralNetMLP(n_output=10, 
                  n_features=X_train.shape[1], 
                  n_hidden=50, 
                  l2=0.1, 
                  l1=0.0, 
                  epochs=1000, 
                  eta=0.001,
                  alpha=0.001,
                  decrease_const=0.00001,
                  minibatches=50, 
                  shuffle=True,
                  random_state=1)

nn.fit(X_train, y_train, print_progress=True)

コスト関数の推移

import matplotlib.pyplot as plt

plt.plot(range(len(nn.cost_)), nn.cost_)
plt.ylim([0, 2000])
plt.ylabel('Cost')
plt.xlabel('Epochs * 50')
plt.tight_layout()
# plt.savefig('./figures/cost.png', dpi=300)
plt.show()

f:id:robonchu:20171214231240p:plain

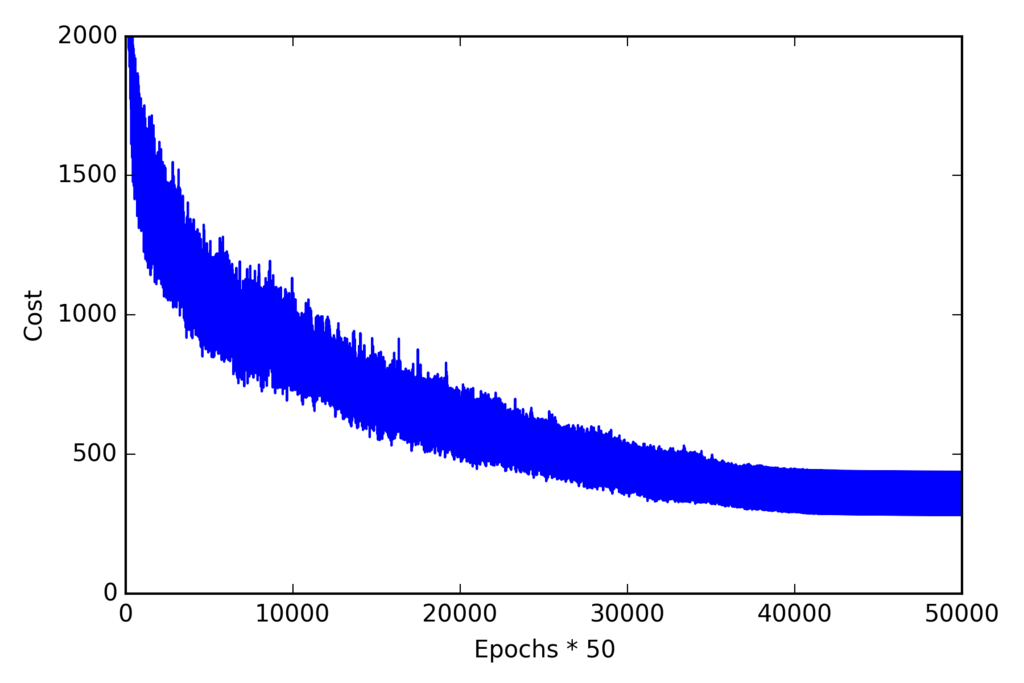
ミニバッチごとに平均化したコスト関数の推移

batches = np.array_split(range(len(nn.cost_)), 1000)
cost_ary = np.array(nn.cost_)
cost_avgs = [np.mean(cost_ary[i]) for i in batches]

plt.plot(range(len(cost_avgs)), cost_avgs, color='red')
plt.ylim([0, 2000])
plt.ylabel('Cost')
plt.xlabel('Epochs')
plt.tight_layout()
#plt.savefig('./figures/cost2.png', dpi=300)
plt.show()

f:id:robonchu:20171214231434p:plain

モデルの性能

y_train_pred = nn.predict(X_train)

if sys.version_info < (3, 0):
    acc = ((np.sum(y_train == y_train_pred, axis=0)).astype('float') /
           X_train.shape[0])
else:
    acc = np.sum(y_train == y_train_pred, axis=0) / X_train.shape[0]

print('Training accuracy: %.2f%%' % (acc * 100))

y_test_pred = nn.predict(X_test)

if sys.version_info < (3, 0):
    acc = ((np.sum(y_test == y_test_pred, axis=0)).astype('float') /
           X_test.shape[0])
else:
    acc = np.sum(y_test == y_test_pred, axis=0) / X_test.shape[0]

print('Test accuracy: %.2f%%' % (acc * 100))

結果

Training accuracy: 97.59%

Test accuracy: 95.62%

上記結果からわずかに過学習していることがわかる。

パラメータの最適化に関して、ベイズ的最適化をためしてみたい。

参考： ベイズ的最適化・実験計画法のお勉強 - 空飛ぶロボットのつくりかた

ベイズ的最適化(Bayesian Optimization)の入門とその応用

予測結果を見てみる

miscl_img = X_test[y_test != y_test_pred][:25]
correct_lab = y_test[y_test != y_test_pred][:25]
miscl_lab = y_test_pred[y_test != y_test_pred][:25]

fig, ax = plt.subplots(nrows=5, ncols=5, sharex=True, sharey=True,)
ax = ax.flatten()
for i in range(25):
    img = miscl_img[i].reshape(28, 28)
    ax[i].imshow(img, cmap='Greys', interpolation='nearest')
    ax[i].set_title('%d) t: %d p: %d' % (i+1, correct_lab[i], miscl_lab[i]))

ax[0].set_xticks([])
ax[0].set_yticks([])
plt.tight_layout()
# plt.savefig('./figures/mnist_miscl.png', dpi=300)
plt.show()

f:id:robonchu:20171216100649p:plain

ネットワークのデバッグ

ニューラルネットワークの実装をする際、かなり複雑になるため、逆伝播が正しく実装されているかを手動で確認できると安心。

方法は、解析的な勾配と数値勾配の比較になる。

以下の図のように数値的に近似された勾配と比較する

f:id:robonchu:20171216121048p:plain

  • 近似式 : (J(w + \epsilon) - J(w - \epsilon)) / 2\epsilon

  • 比較の仕方 : 正規化されたL2ベクトルノルムが計算することが推奨

    • 相対誤差 = \frac{|| J _n - J_a ||_2}{ || J_n||_2 + ||J_a||_2}

  • 比較時のしきい値はモデルに依存するため、適切に設定する必要がある

参考： ノルムの意味とL1，L2，L∞ノルム | 高校数学の美しい物語

実装

import numpy as np
from scipy.special import expit
import sys


class MLPGradientCheck(object):
    """ Feedforward neural network / Multi-layer perceptron classifier.

    Parameters
    ------------
    n_output : int
        Number of output units, should be equal to the
        number of unique class labels.
    n_features : int
        Number of features (dimensions) in the target dataset.
        Should be equal to the number of columns in the X array.
    n_hidden : int (default: 30)
        Number of hidden units.
    l1 : float (default: 0.0)
        Lambda value for L1-regularization.
        No regularization if l1=0.0 (default)
    l2 : float (default: 0.0)
        Lambda value for L2-regularization.
        No regularization if l2=0.0 (default)
    epochs : int (default: 500)
        Number of passes over the training set.
    eta : float (default: 0.001)
        Learning rate.
    alpha : float (default: 0.0)
        Momentum constant. Factor multiplied with the
        gradient of the previous epoch t-1 to improve
        learning speed
        w(t) := w(t) - (grad(t) + alpha*grad(t-1))
    decrease_const : float (default: 0.0)
        Decrease constant. Shrinks the learning rate
        after each epoch via eta / (1 + epoch*decrease_const)
    shuffle : bool (default: False)
        Shuffles training data every epoch if True to prevent circles.
    minibatches : int (default: 1)
        Divides training data into k minibatches for efficiency.
        Normal gradient descent learning if k=1 (default).
    random_state : int (default: None)
        Set random state for shuffling and initializing the weights.

    Attributes
    -----------
    cost_ : list
        Sum of squared errors after each epoch.

    """
    def __init__(self, n_output, n_features, n_hidden=30,
                 l1=0.0, l2=0.0, epochs=500, eta=0.001,
                 alpha=0.0, decrease_const=0.0, shuffle=True,
                 minibatches=1, random_state=None):

        np.random.seed(random_state)
        self.n_output = n_output
        self.n_features = n_features
        self.n_hidden = n_hidden
        self.w1, self.w2 = self._initialize_weights()
        self.l1 = l1
        self.l2 = l2
        self.epochs = epochs
        self.eta = eta
        self.alpha = alpha
        self.decrease_const = decrease_const
        self.shuffle = shuffle
        self.minibatches = minibatches

    def _encode_labels(self, y, k):
        """Encode labels into one-hot representation

        Parameters
        ------------
        y : array, shape = [n_samples]
            Target values.

        Returns
        -----------
        onehot : array, shape = (n_labels, n_samples)

        """
        onehot = np.zeros((k, y.shape[0]))
        for idx, val in enumerate(y):
            onehot[val, idx] = 1.0
        return onehot

    def _initialize_weights(self):
        """Initialize weights with small random numbers."""
        w1 = np.random.uniform(-1.0, 1.0,
                               size=self.n_hidden*(self.n_features + 1))
        w1 = w1.reshape(self.n_hidden, self.n_features + 1)
        w2 = np.random.uniform(-1.0, 1.0,
                               size=self.n_output*(self.n_hidden + 1))
        w2 = w2.reshape(self.n_output, self.n_hidden + 1)
        return w1, w2

    def _sigmoid(self, z):
        """Compute logistic function (sigmoid)

        Uses scipy.special.expit to avoid overflow
        error for very small input values z.

        """
        # return 1.0 / (1.0 + np.exp(-z))
        return expit(z)

    def _sigmoid_gradient(self, z):
        """Compute gradient of the logistic function"""
        sg = self._sigmoid(z)
        return sg * (1.0 - sg)

    def _add_bias_unit(self, X, how='column'):
        """Add bias unit (column or row of 1s) to array at index 0"""
        if how == 'column':
            X_new = np.ones((X.shape[0], X.shape[1] + 1))
            X_new[:, 1:] = X
        elif how == 'row':
            X_new = np.ones((X.shape[0]+1, X.shape[1]))
            X_new[1:, :] = X
        else:
            raise AttributeError('`how` must be `column` or `row`')
        return X_new

    def _feedforward(self, X, w1, w2):
        """Compute feedforward step

        Parameters
        -----------
        X : array, shape = [n_samples, n_features]
            Input layer with original features.
        w1 : array, shape = [n_hidden_units, n_features]
            Weight matrix for input layer -> hidden layer.
        w2 : array, shape = [n_output_units, n_hidden_units]
            Weight matrix for hidden layer -> output layer.

        Returns
        ----------
        a1 : array, shape = [n_samples, n_features+1]
            Input values with bias unit.
        z2 : array, shape = [n_hidden, n_samples]
            Net input of hidden layer.
        a2 : array, shape = [n_hidden+1, n_samples]
            Activation of hidden layer.
        z3 : array, shape = [n_output_units, n_samples]
            Net input of output layer.
        a3 : array, shape = [n_output_units, n_samples]
            Activation of output layer.

        """
        a1 = self._add_bias_unit(X, how='column')
        z2 = w1.dot(a1.T)
        a2 = self._sigmoid(z2)
        a2 = self._add_bias_unit(a2, how='row')
        z3 = w2.dot(a2)
        a3 = self._sigmoid(z3)
        return a1, z2, a2, z3, a3

    def _L2_reg(self, lambda_, w1, w2):
        """Compute L2-regularization cost"""
        return (lambda_/2.0) * (np.sum(w1[:, 1:] ** 2) +
                                np.sum(w2[:, 1:] ** 2))

    def _L1_reg(self, lambda_, w1, w2):
        """Compute L1-regularization cost"""
        return (lambda_/2.0) * (np.abs(w1[:, 1:]).sum() +
                                np.abs(w2[:, 1:]).sum())

    def _get_cost(self, y_enc, output, w1, w2):
        """Compute cost function.

        Parameters
        ----------
        y_enc : array, shape = (n_labels, n_samples)
            one-hot encoded class labels.
        output : array, shape = [n_output_units, n_samples]
            Activation of the output layer (feedforward)
        w1 : array, shape = [n_hidden_units, n_features]
            Weight matrix for input layer -> hidden layer.
        w2 : array, shape = [n_output_units, n_hidden_units]
            Weight matrix for hidden layer -> output layer.

        Returns
        ---------
        cost : float
            Regularized cost.

        """
        term1 = -y_enc * (np.log(output))
        term2 = (1.0 - y_enc) * np.log(1.0 - output)
        cost = np.sum(term1 - term2)
        L1_term = self._L1_reg(self.l1, w1, w2)
        L2_term = self._L2_reg(self.l2, w1, w2)
        cost = cost + L1_term + L2_term
        return cost

    def _get_gradient(self, a1, a2, a3, z2, y_enc, w1, w2):
        """ Compute gradient step using backpropagation.

        Parameters
        ------------
        a1 : array, shape = [n_samples, n_features+1]
            Input values with bias unit.
        a2 : array, shape = [n_hidden+1, n_samples]
            Activation of hidden layer.
        a3 : array, shape = [n_output_units, n_samples]
            Activation of output layer.
        z2 : array, shape = [n_hidden, n_samples]
            Net input of hidden layer.
        y_enc : array, shape = (n_labels, n_samples)
            one-hot encoded class labels.
        w1 : array, shape = [n_hidden_units, n_features]
            Weight matrix for input layer -> hidden layer.
        w2 : array, shape = [n_output_units, n_hidden_units]
            Weight matrix for hidden layer -> output layer.

        Returns
        ---------
        grad1 : array, shape = [n_hidden_units, n_features]
            Gradient of the weight matrix w1.
        grad2 : array, shape = [n_output_units, n_hidden_units]
            Gradient of the weight matrix w2.

        """
        # backpropagation
        sigma3 = a3 - y_enc
        z2 = self._add_bias_unit(z2, how='row')
        sigma2 = w2.T.dot(sigma3) * self._sigmoid_gradient(z2)
        sigma2 = sigma2[1:, :]
        grad1 = sigma2.dot(a1)
        grad2 = sigma3.dot(a2.T)

        # regularize
        grad1[:, 1:] += self.l2 * w1[:, 1:]
        grad1[:, 1:] += self.l1 * np.sign(w1[:, 1:])
        grad2[:, 1:] += self.l2 * w2[:, 1:]
        grad2[:, 1:] += self.l1 * np.sign(w2[:, 1:])

        return grad1, grad2

    def _gradient_checking(self, X, y_enc, w1, w2, epsilon, grad1, grad2):
        """ Apply gradient checking (for debugging only)

        Returns
        ---------
        relative_error : float
          Relative error between the numerically
          approximated gradients and the backpropagated gradients.

        """
        num_grad1 = np.zeros(np.shape(w1))
        epsilon_ary1 = np.zeros(np.shape(w1))
        for i in range(w1.shape[0]):
            for j in range(w1.shape[1]):
                epsilon_ary1[i, j] = epsilon
                a1, z2, a2, z3, a3 = self._feedforward(X,
                                                       w1 - epsilon_ary1, w2)
                cost1 = self._get_cost(y_enc, a3, w1-epsilon_ary1, w2)
                a1, z2, a2, z3, a3 = self._feedforward(X,
                                                       w1 + epsilon_ary1, w2)
                cost2 = self._get_cost(y_enc, a3, w1 + epsilon_ary1, w2)
                num_grad1[i, j] = (cost2 - cost1) / (2.0 * epsilon)
                epsilon_ary1[i, j] = 0

        num_grad2 = np.zeros(np.shape(w2))
        epsilon_ary2 = np.zeros(np.shape(w2))
        for i in range(w2.shape[0]):
            for j in range(w2.shape[1]):
                epsilon_ary2[i, j] = epsilon
                a1, z2, a2, z3, a3 = self._feedforward(X, w1,
                                                       w2 - epsilon_ary2)
                cost1 = self._get_cost(y_enc, a3, w1, w2 - epsilon_ary2)
                a1, z2, a2, z3, a3 = self._feedforward(X, w1,
                                                       w2 + epsilon_ary2)
                cost2 = self._get_cost(y_enc, a3, w1, w2 + epsilon_ary2)
                num_grad2[i, j] = (cost2 - cost1) / (2.0 * epsilon)
                epsilon_ary2[i, j] = 0

        num_grad = np.hstack((num_grad1.flatten(), num_grad2.flatten()))
        grad = np.hstack((grad1.flatten(), grad2.flatten()))
        norm1 = np.linalg.norm(num_grad - grad)
        norm2 = np.linalg.norm(num_grad)
        norm3 = np.linalg.norm(grad)
        relative_error = norm1 / (norm2 + norm3)
        return relative_error

    def predict(self, X):
        """Predict class labels

        Parameters
        -----------
        X : array, shape = [n_samples, n_features]
            Input layer with original features.

        Returns:
        ----------
        y_pred : array, shape = [n_samples]
            Predicted class labels.

        """
        if len(X.shape) != 2:
            raise AttributeError('X must be a [n_samples, n_features] array.\n'
                                 'Use X[:,None] for 1-feature classification,'
                                 '\nor X[[i]] for 1-sample classification')

        a1, z2, a2, z3, a3 = self._feedforward(X, self.w1, self.w2)
        y_pred = np.argmax(z3, axis=0)
        return y_pred

    def fit(self, X, y, print_progress=False):
        """ Learn weights from training data.

        Parameters
        -----------
        X : array, shape = [n_samples, n_features]
            Input layer with original features.
        y : array, shape = [n_samples]
            Target class labels.
        print_progress : bool (default: False)
            Prints progress as the number of epochs
            to stderr.

        Returns:
        ----------
        self

        """
        self.cost_ = []
        X_data, y_data = X.copy(), y.copy()
        y_enc = self._encode_labels(y, self.n_output)

        delta_w1_prev = np.zeros(self.w1.shape)
        delta_w2_prev = np.zeros(self.w2.shape)

        for i in range(self.epochs):

            # adaptive learning rate
            self.eta /= (1 + self.decrease_const*i)

            if print_progress:
                sys.stderr.write('\rEpoch: %d/%d' % (i+1, self.epochs))
                sys.stderr.flush()

            if self.shuffle:
                idx = np.random.permutation(y_data.shape[0])
                X_data, y_enc = X_data[idx], y_enc[idx]

            mini = np.array_split(range(y_data.shape[0]), self.minibatches)
            for idx in mini:

                # feedforward
                a1, z2, a2, z3, a3 = self._feedforward(X[idx],
                                                       self.w1,
                                                       self.w2)
                cost = self._get_cost(y_enc=y_enc[:, idx],
                                      output=a3,
                                      w1=self.w1,
                                      w2=self.w2)
                self.cost_.append(cost)

                # compute gradient via backpropagation
                grad1, grad2 = self._get_gradient(a1=a1, a2=a2,
                                                  a3=a3, z2=z2,
                                                  y_enc=y_enc[:, idx],
                                                  w1=self.w1,
                                                  w2=self.w2)

                # start gradient checking
                grad_diff = self._gradient_checking(X=X_data[idx],
                                                    y_enc=y_enc[:, idx],
                                                    w1=self.w1,
                                                    w2=self.w2,
                                                    epsilon=1e-5,
                                                    grad1=grad1,
                                                    grad2=grad2)


                if grad_diff <= 1e-7:
                    print('Ok: %s' % grad_diff)
                elif grad_diff <= 1e-4:
                    print('Warning: %s' % grad_diff)
                else:
                    print('PROBLEM: %s' % grad_diff)

                # update weights; [alpha * delta_w_prev] for momentum learning
                delta_w1, delta_w2 = self.eta * grad1, self.eta * grad2
                self.w1 -= (delta_w1 + (self.alpha * delta_w1_prev))
                self.w2 -= (delta_w2 + (self.alpha * delta_w2_prev))
                delta_w1_prev, delta_w2_prev = delta_w1, delta_w2

        return self

nn_check = MLPGradientCheck(n_output=10, 
                            n_features=X_train.shape[1], 
                            n_hidden=10, 
                            l2=0.0, 
                            l1=0.0, 
                            epochs=10, 
                            eta=0.001,
                            alpha=0.0,
                            decrease_const=0.0,
                            minibatches=1, 
                            shuffle=False,
                            random_state=1)

nn_check.fit(X_train[:5], y_train[:5], print_progress=False)

結果

Ok: 2.55068505986e-10
Ok: 2.93547837023e-10
Ok: 2.37449571314e-10
Ok: 3.08194323691e-10
Ok: 3.38249440642e-10
Ok: 3.57890221135e-10
Ok: 2.19231256383e-10
Ok: 2.36583740198e-10
Ok: 3.43584860701e-10
Ok: 2.13345208113e-10

Tips

  • チェックのコードはできるだけシンプルに

  • 計算コストが高いためデバッグ目的のみで使用しよう

ニューラルネットの収束

以下の図のように次元数が多いため、コスト局面は複雑で適切に学習を行うためには、パラメータ（学習率）の調節が重要。

f:id:robonchu:20171216162938p:plain

おまけ

手書き文字のデータを見ると文字が歪んでいたり、傾いていたりする

歪補正(deskew)

共分散の大きさを用いて、アフィン変換で歪みを補正。

データの前処理でこのようなことをおこなうことで学習結果がよくなったりする。

参考：

せん断写像 - Wikipedia

アフィン変換とは - 大人になってからの再学習

Deskewing

teaching-ncso/91-mnist-deskew.ipynb at master · tmbdev/teaching-ncso · GitHub

3層パーセプトロン

参考： Pythonで3層パーセプトロンの誤差逆伝播を実装してみる - TadaoYamaokaの日記

感想

深層学習で認識や音声など様々な分野での性能は向上するが、様々な汎用的なタスクをひとつのモデルでこなすのは現状は難しく、人間による前処理やタスクに適切なモデル選択、設計が必要。

なので、思考や動作を伴う汎用、複合的なタスクをロボットやシステムができるようになるのはもう少し先という印象。

おまけ

CNN

機械学習のお勉強（ＣＮＮ） - 空飛ぶロボットのつくりかた

定番のConvolutional Neural Networkをゼロから理解する - DeepAge

RNN

RNN：時系列データを扱うRecurrent Neural Networksとは - DeepAge

全体参考

バイトオーダ - ビッグエンディアン/リトルエディアン