数学のお勉強（1）~クオータニオン~

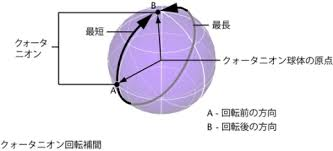
参考：クォータニオンの回転補間：掲示板:シムダンス「四次元能」｜Beach - ビーチ

やりたいこと

クオータニオンを理解する

教科書

• SBクリエイティブ:ゲームアプリの数学

↓　素晴らしくわかりやすい。

• 【Unity道場 博多スペシャル 2017】クォータニオン完全マスター - YouTube

• 【Unity道場スペシャル 2017博多】クォータニオン完全マスター

• クォータニオンで回転を表現する定義にθ/2が使用される理由

回転行列の問題

1. ジンバルロック（特異点がある）

2. 行列計算での処理負荷が重い

3. 回転の補間が難しい

クオータニオンの利点

1. ジンバルロックがない

2. 計算負荷が低い

3. 2つの回転同士のスムーズな補間が表現できる

4. x,y,z軸に限らない任意の回転軸での回転が簡単にできる

複素数について

虚数単位

i ** 2 = -1

複素数

a + b * i

複素平面

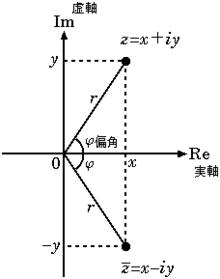
参考： 複素平面 - Wikipedia

複素数の行列表現

I = numpy.array([[0, -1], [1, 0]])

E = numpy.array([[1, 0], [0, 1]])

I ** 2 = - E

Z = a*E + b*I = numpy.array([[a, -b], [b, a]])

Z = numpy.array([[numpy.cos(theta), -numpy.sin(theta)], [numpy.siN(theta), numpy.cos(theta)]]) * numpy.array([[r, 0], [0, r]])

複素数の場合、乗法の交換法則・結合法則・分配法則を満たす

共役

z' = a - b * i

z * z' = || z || ** 2

複素数のすごさ

「複素数平面における点の回転」は「複素数のかけ算」に対応している。

「回転を足す」と「複素数を掛ける」は同じ意味！

たとえば、単位円でiを掛けていくと90度ずつ回転する。めちゃ便利。

参考：

• 【Unity道場スペシャル 2017博多】クォータニオン完全マスター

• 複素数平面における回転と極形式 | 高校数学の美しい物語

二重数について

冪零元

epsilon**n = 0

二重数

z = a + b*epsilon

epsilon = numpy.array([[0, 1], [0, 0]])

Z = a + b*epsilon = numpy.array([[a, b], [0, a]])

bを二重部という

複素数の場合、乗法の交換法則・結合法則・分配法則を満たす

クオータニオン

複素数の拡張として考えることができる

q = w + x*i + y*j + z*k  # i,j,kは虚軸 

• 複素数は1とiという2つの線形独立な基底ベクトルで平面を表現

• クオータニオンは1,i,j,kという4つの線形独立な基底ベクトルによる4次元空間を表す

基底i,j,kの関係

i**2 = j**2 = k**2 = -i*j*k = -1

i*j = k

j*i = -k

j * k = i

k * j = -i

k * i = j

i * k = -j

交換法則はなりたたない

クオータニオンはw,x,y,zの組として、

q = [w, x, y, z]

と表記されることがおおい

クオータニオンの演算

共役

q' = [w, -x, -y, -z]

大きさ

v = (x, y, z)

|q| = sqrt(w**2 + |v|**2)

乗算

ベクトル部の内積と外積をもちいて以下のように表される

q0q1 = [w0 * w1 - v0 * v1 ,  w0 * v1 + w1 * v0 + v0 ✕ v1]

内積

q0 * q1 = w0 * w1 + v0 * v1

逆数

q**-1 = q' / |q|**2

単位クオータニオンでは、共役を求めれば逆数が求まることがわかる

行列表現

i = numpy.array([[0, 0, 0, 1], [0, 0, -1, 0],[0, 1, 0, 0],[-1, 0, 0, 0]])

j = numpy.array([[0, 0, 1, 0], [0, 0, 0, 1],[-1, 0, 0, 0],[0, -1, 0, 0]])

k = numpy.array([[0, -1, 0, 0], [1, 0, 0, 0],[0, 0, 0, 1],[0, 0, -1, 0]])

3D回転

回転

あるベクトルpを単位クオータニオンを用いて3次元空間で回転を表現する方法

p' = q * p * q**-1

p' = [0, v]

q = [qw, qv]  # qv:回転軸

p = [0, pv]

qw = +- numpy.cos(theta/2.0)

qv = +- numpy.sin(theta/2)*u  # u:qvと同じ方向の単位ベクトル

上記をまとめると、3次元の回転はクオータニオンを使って以下の式で表される

p' = q * p * q**-1

q = [numpy.cos(theta/2.0)  numpy.sin(theta/2.0)*u]

pを単位クオータニオンqで回転したあと、rをつかって回転させる場合、

r*(q*p*q**-1)*r**-1=(rq)*p*(q`r`)=(rq)*p*(rq)`

となり、あらかじめクオータニオンrqを計算してクオータニオンsとして合成しておけば、回転の合成を行うことができる

クオータニオンを使えばどんな回転も一発で表現可能

デュアルクオータニオン

定義

回転のみならず、剛体変換（回転と平行移動）を表現できる。

クオータニオンの二重数である

q^ = r + d * epsilon  # r,d: クオータニオン、epsilon:零冪元

所感

わかったようなわからないような。。。とりあえずハミルトン大先生すごい笑

まだ正直、理解しきれてない気がする。追記していこう : )